√完了しました! parabola congruent to y=x^2 216216-Parabola congruent to y=x^2
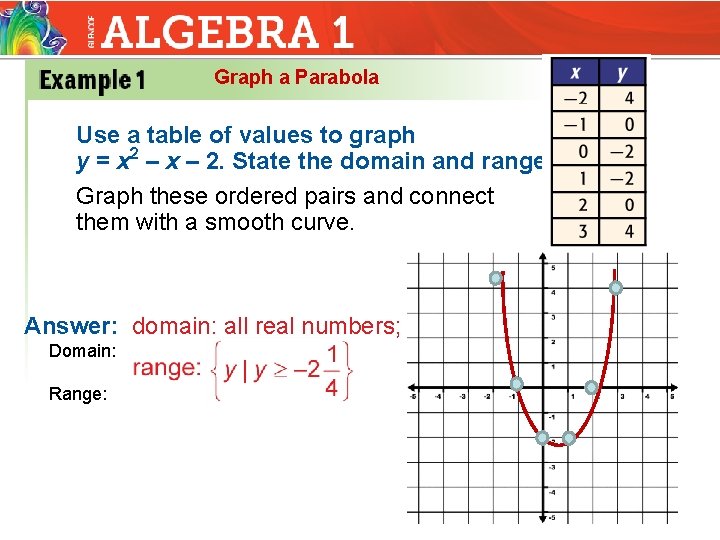
Consider a parabola P that is congruent to y=x^2, opens upward,and has its vertex at (2,4) Now find the equation of a new parabola that results if P is A stretched vertically by a factor of 5 B compressed by a factor of 2New parabola should be congruent (the same shape and size) to y = x2, with the same vertex, except it should open downward so its vertex will be its highest point Record the Find a way to change the equation to make the y = x2 parabola move 3 units to the left and stretch vertically, as in part (c)Your new parabola might look like y = 4x2Graph the parabola, y =x^21 by finding the turning point and using a table to find values for x and y
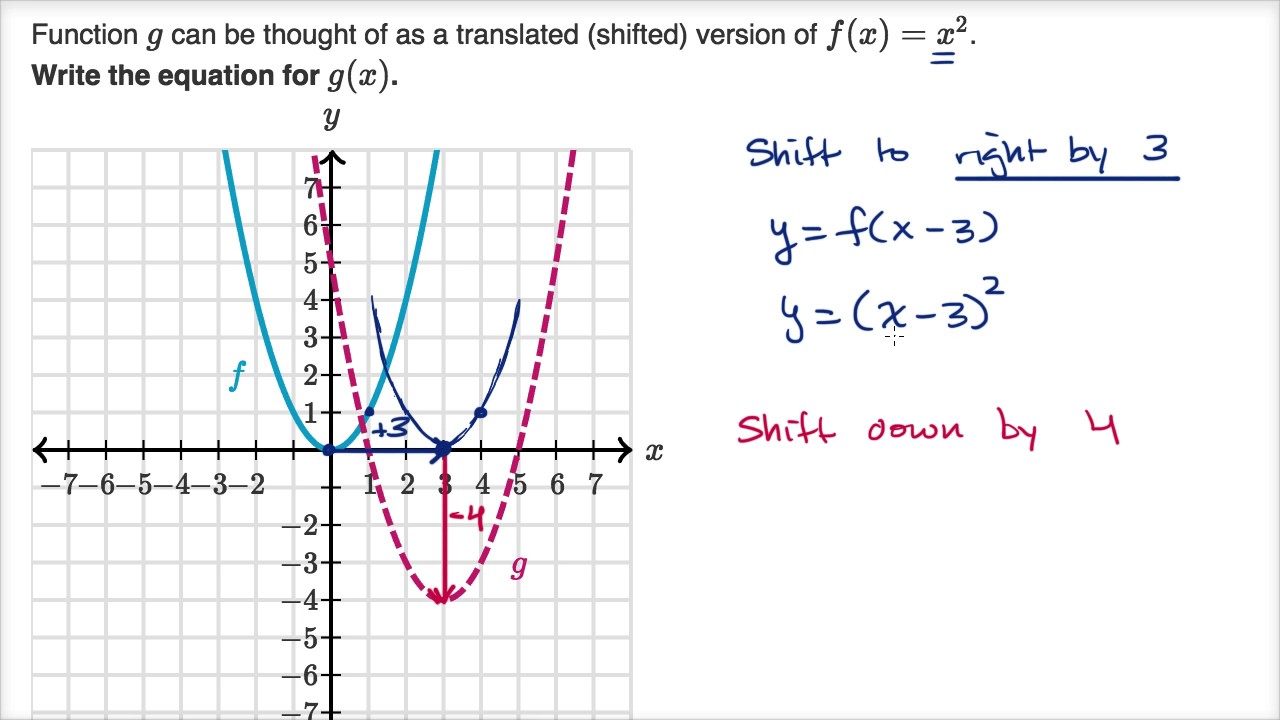
Shifting Parabolas Video Khan Academy
Parabola congruent to y=x^2
Parabola congruent to y=x^2-10 CHAPTER 16 PARTIAL DERIVATIVES Figure 1617 often more useful to sketch a few of its level curves than to sketch that surface Each level curve is the projection of aEvery parabola has an axis of symmetry which is the line that divides the graph into two perfect halves On this page, we will practice drawing the axis on a graph, learning the formula, stating the equation of the axis of symmetry when we know the parabola's equation




Vertical And Horizontal Transformations Read Algebra Ck 12 Foundation
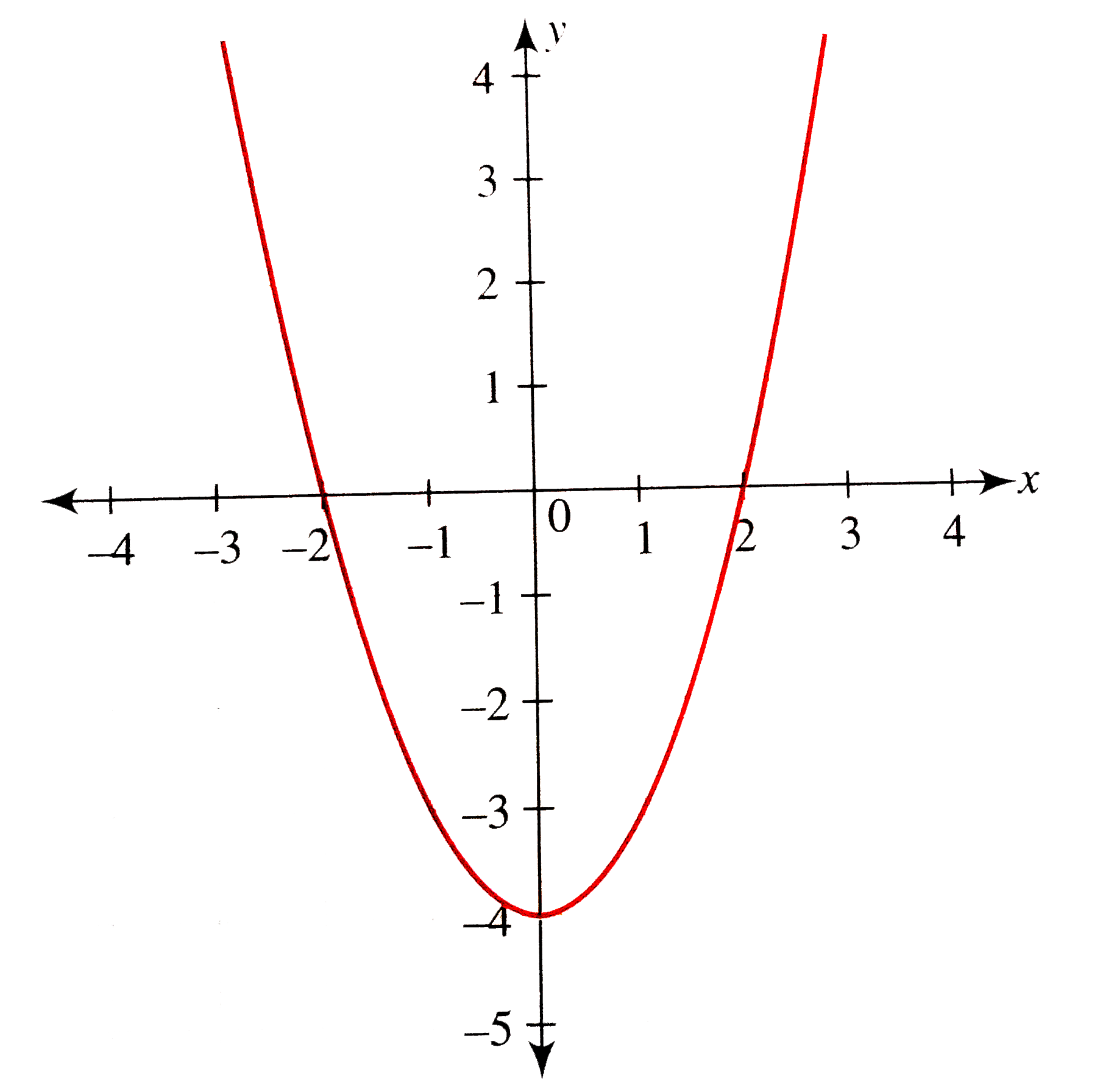
The coefficient of the #color(green)(x^2# term is Positive and hence, our Parabola Opens Upward, and it has a minimum Please refer to the image of the graph below to verify our solutions The Axis of symmetry of a parabola is a vertical line that divides the parabola into two congruent halves_Mpm2dc all of unit 4markeddocx Mpm2dc all of unit 4 Your mark for this unit is 735\/87 = 84 Mpm2dc unit 41 14\/18 41 a The parabola definedThe axis of symmetry is the line that goes through the vertex and divides the parabola into congruent halves It is located at x = ±2 Find the yintercept In the equation y = x2 í 4x 5, a = 1, b = ±4, and c = 5 The xcoordinate of the vertex is
When the basic parabola y = x2 is reflected in the x axis, the point (3, 9), for example, is reflected to the point (3, 9) Indeed the general point (a, a2) becomes (a, − a2) and so the equation satisfied by these points is y = −x2 We can confirm this with a table of values0 up (0,0) x 0 Yes y x2 2 y x2 4 y x2 1 y x2 and y ax2 Clear all previous equations from your calculator Repeat part A for the followingParabolas can have both xintercepts and y intercepts yintercept As you can see from the picture below, the yintercept is the point at which the parabola intercepts the yaxis xintercepts The xintercepts are the points or the point at which the parabola intersects the xaxis A parabola can have either 2,1 or zero real x intercepts
math Consider a parabola P that is congruent (has the same shape) to y=x^2, opens upward, and has vertex (2,3) Now find the equation of a new parabola that results if P is Compressed to a factor of 1/2 Translated 2 units to the left Parabola described by y = 2x2 is narrower than the parabola described by y = x2 Smaller the coefficient of x2 wider the curveWhile a parabola is always symmetric about the vertical line through the vertex (the parabola's "axis"), the Tchart points might not be symmetric In particular, the Tchart points will not "match" if the x coordinate of the vertex is something other than a



How To Find The Range Of A Parabola And What Is It With The Y Is Less Than Or Equal To Number Thing Quora



Http Blessedmotherteresa Typepad Com Files Graphingquadratics Day3 Pdf
2x =4a dy/dx = 4am where m is slope of the tangent or x=2am Using this value in x^2 =4a^2m^2 = 4ay gives y = am^2 That means the tangent touches the parabola at (2am,am^2) Now equation of tangent is y=mxc and it passes the above point so am^2 = 2am^2c or c= am^2Thus, a parabola is a conic section Consider a parabola P that is congruent to y = x 2, opens upward, and has vertex (–1, 3) Now find the equation of a new parabola that results if p is reflected in the x–axis and translated 3 units down
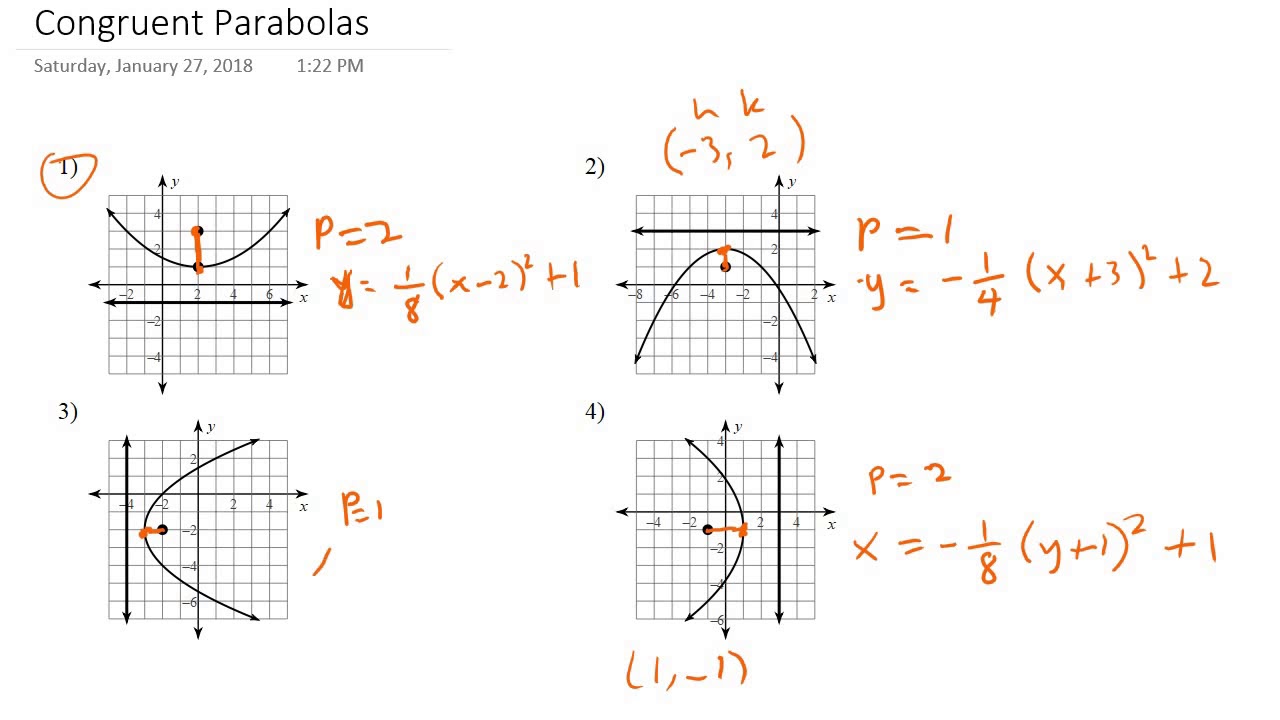



Congruent Parabolas Youtube
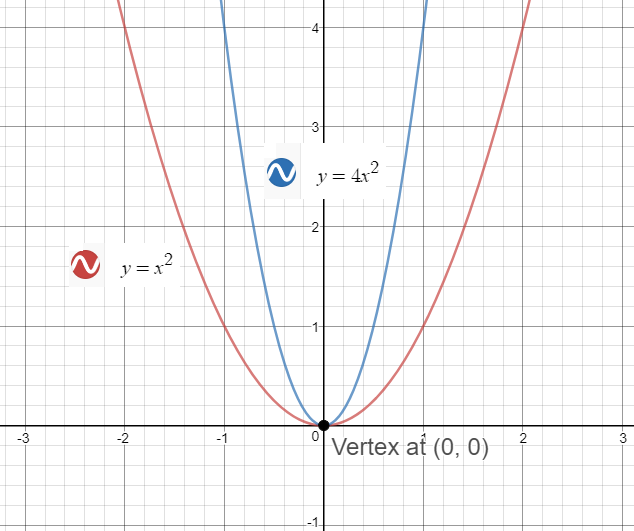



How To Graph A Parabola Y 4x 2 Socratic
Y (x 21) 2 y (x 2)2 1 The inequality is The inequality is yx2 4 The curve is solidFree Parabola calculator Calculate parabola foci, vertices, axis and directrix stepbystep This website uses cookies to ensure you get the best experienceState the equation of a parabola congruent to y = 3x2 that has been translated 8 units left and 5 units down from y = 3x2 State the equation of a parabola congruent to y = 2x2 that has been translated 10 units right and 2 units up from y = 2x2 A parabola is congruent to y = x2 Its vertex is (3, 5) State its equation State the vertex and



1
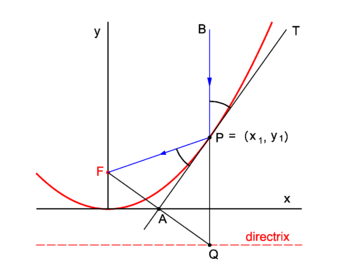



Parabola Knowino
A parabola that opens downward, is congruent to y=X 2 , and has its vertex at (3, 0) find the equation? f Is the parabola in this question (with focus point (1, 1) and directrix y = – 3) congruent to a parabola with focus (2, 3) and directrix y = – 1?A hyperbolic paraboloid (not to be confused with a hyperboloid) is a doubly ruled surface shaped like a saddleIn a suitable coordinate system, a hyperbolic paraboloid can be represented by the equation 6 = In this position, the hyperbolic paraboloid opens downward along the xaxis and upward along the yaxis (that is, the parabola in the plane x = 0 opens upward and the parabola
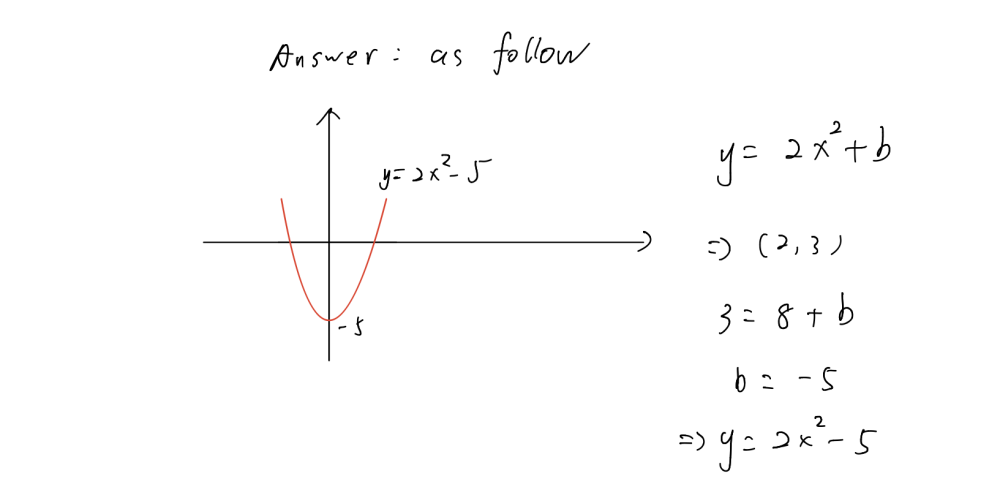



Vrite The Equation Of A Parabola That Matches The Gauthmath
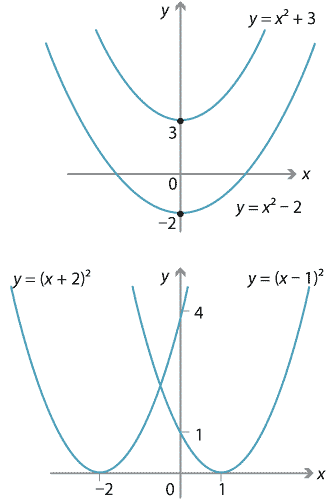



Content Transformations Of The Parabola
The Vertex of the Parabola In this case, we need to find the equation of the graph which is congruent to another graph, thus we know that the coefficient of theAbout Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us CreatorsA Sketch the graphs on the same axes Label each parabola with its equation b Describe how the value of k in changes the graph of c What happens to the xcoordinates of all points on Congruent to ?




5 Consider The Parabola Of The Function P X Below P X 3 6 A Write The Equation Of Homeworklib




Vertical And Horizontal Transformations Read Algebra Ck 12 Foundation
A Write down the equation of the parabola obtained when the graph of y = x2 is translated 3 units to the left Sketch the parabola b Describe the transformation required to move the parabola y = (x 3)2 to y = (x – 2)2 Sketch the parabola General Translations We can combine the two transformations and shift parabolas up or down and thenA parabola is congruent to y=x^2 and has xintercepts 1 and 5 determine the coordinates of the vertex Answer by Fombitz () (Show Source) You can put this solution on YOUR website!A parabola is the locus of points which are equidistant from a fixed point, the focus, and a fixed line, the directrix To find the equation of such a curve construct a coordinate system on the plane so that the focus is the point (0,p) and the directrix is the horizontal line y = p A point (x,y) is thus on the curve if and only if the
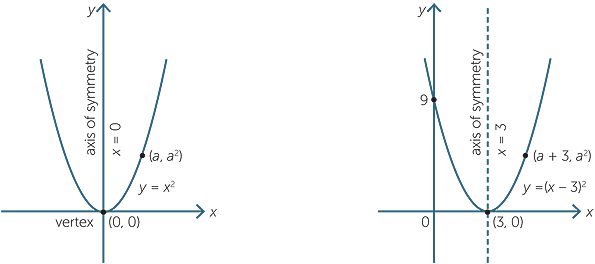



Quadratic Function
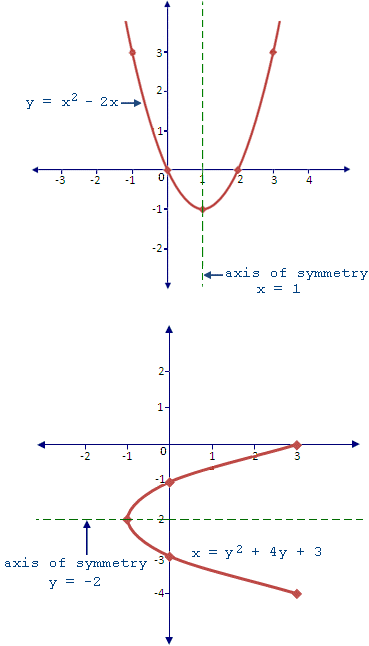



Axis Of Symmetry Of A Parabola
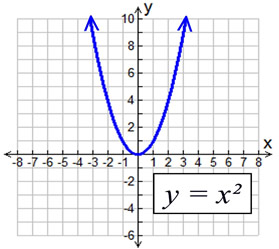
Graph y=x^2 Find the properties of the given parabola Tap for more steps Rewrite the equation in vertex form Tap for more steps Complete the square for The directrix of a parabola is the horizontal line found by subtracting from the ycoordinate of the vertex if the parabolaWrite the equation with y 0 on one side y 0 = x 0 2 4 − x 0 5 This equation in ( x 0, y 0) is true for all other values on the parabola and hence we can rewrite with ( x, y) So, the equation of the parabola with focus ( 2, 5) and directrix is y = 3 is y = x 2 4 − x 5 Arc of the parabola y = x 2 I was studying line integral for some pdfs and came up with the following question ∫ γ ( x − 2 y 2) d y, γ is the arc of the parabola y = x 2 from ( − 2, 4) to ( 1, 1) I used the parameterization γ ( t) = ( t, t 2) , γ ′ ( t) = ( 1, 2 t) e ‖ γ ′ ( t) ‖ = 1 4 t 2, but when i do ∫ − 2 1
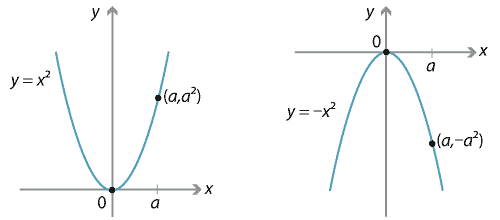



Content Transformations Of The Parabola
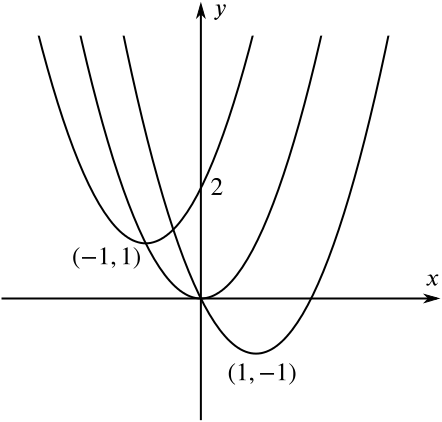



Solution Into How Many Regions Do These Parabolas Divide The Plane Quadratics Underground Mathematics
We defined the vertex and the axis of symmetry of this graph and we're going to I mean the whole point of doing this problem is so that you understand what the vertex and axis of symmetry is and just as a bit of a refresher if a parabola looks like this the vertex is the lowest point here it's this minimum point here for an upwardopening parabola if the parabola opens downward like thisIf a) it undergoes a horizontal translation of 3 units left and a vertical translation 4 units down and is congruent to y = v=7x² Y=x 2 Bu Left Left 4 w = 4 2 so y=(x3) 2_4 a so 1 Y = (x3) ² 4 5a) 2 marks b) the parabola opens upwards and is stretched vertically by a factor of 52 Given y = 3x2 1) Write the equation of a parabola that contains the point (2, 12) that is congruent to the parabola that is given Describe the series of transformations that would move the given parabola to your parabola 2) Write the equation of a parabola that contains the point (0, 8) that is congruent to the parabola that is given




Quadratic Equation Congruent To Parabola Pass Through Point With Y Intercept As Another Curve Youtube
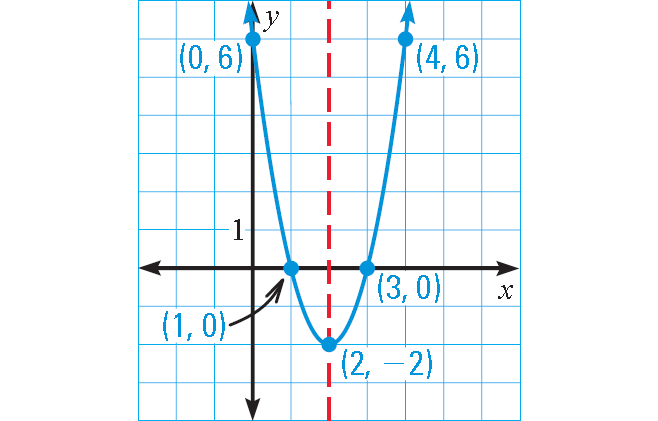



Graphing Quadratic Functions Parabola
A She should shift it 3 units to the left B 40 Melissa graphed a parabola with vertex at congruent to the parabola and opening downward Which graph shows Melissa's parabola?Trigonometry questions and answers consider a parabola P that is congruent to y=x2, opens upward and has a vertex of (1,3) Now find the equation of the new parabola that results it P is reflected in the xaxis and translated 3 units down Question consider a parabola P that is congruent to y=x2, opens upward and has a vertex of (1,3)Parabola Calculator This calculator will find either the equation of the parabola from the given parameters or the axis of symmetry, eccentricity, latus rectum, length of the latus rectum, focus, vertex, directrix, focal parameter, xintercepts, yintercepts of the entered parabola To graph a parabola, visit the parabola grapher (choose the



Http Gerckemath Weebly Com Uploads 3 0 9 5 M1l34 35 Cca2 Notes Pdf




Pin On Images
What is the y intercept in y=(x2)^22 of a parabola is a vertical line that divides the parabola into two congruent halves Upgrade to remove ads Only $399/month Subjects Arts and Humanities Languages Math Science Social ScienceWe're going to explore the equation of a parabola y=a x 2 b xc for different values of a, b, and c First, let's look at the graph of a basic parabola y=x 2, where a =1, b =0, and c =0 Notice the graph opens up, the vertex is at x=0, and the yintercept is at y=0Question Write an equation for a parabola that is congruent to the graph of y = x 2, opens downward, and has its vertex at (3,1) check_circle



1



Exploration Of Parabolas
The first parabola is translated horizontally to the right by two units and the second parabola is translated down by 3 units, so they each are congruent to the original parabola Exercise 2 Sketch the graph of y = x 2 and the two parabolas you created on the same coordinate axes Answer Exercise 3 Write the equation of two parabolas thatThe focus of a parabola can be found by adding to the ycoordinate if the parabola opens up or down Substitute the known values of , , and into the formula and simplify Find the axis of symmetry by finding the line that passes through the vertex and the focus Find the directrixWrite an equation of a parabola that satisfies each set of conditions a) opens upward, congruent to y=x^2and vertex (0, 4) b) opens upward, congruent to y=x^2
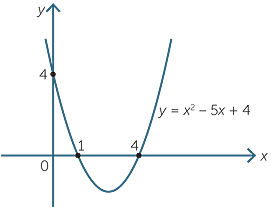



Quadratic Function



Consider A Parabola Math Y X 2 Math The Line That Goes Through The Point 0 3 2 And Is Orthogonal To A Tangent Line To The Part Of Parabola Math Y X 2 Math With Math X 0 Math Is Math Y Ax 3 2 Math What
Explain Answer g Is the parabola in this question (with focus point (1, 1) and directrix y = – 3) congruent to the parabola with equation given by y = x 2?A parabola is the planar curve formed by the points that lie as far from a given line (the directrix) as from a given point (the focus)Alternatively, a parabola is the curve you get when intersecting a right circular cone with a plane parallel to a generator of the cone (a line on the cone which goes through its apex); 6 The idea is to look at a single parabola of the form y = x 2 r, and determine r such that the parabola is tangent to the lines y = ± 3 x This r will be the radius of the inscribed circle See the following figure, which only shows the top and bottom parabolas, but adds the lines To this end, we compute the derivative




Graphing Quadratic Functions Lesson Article Khan Academy



Solution Find The Equation Of The Parabola With Vertex 4 4 The Parabola Opens Upwards And Is Congruent To Y 1 2x 2 Can You Please Help Me Thanks So Much In Advance
3 Ana drew the parent graph of y=x2 How should she transform that graph to produce the graph of y=4(x −3)2?14 A parabola is congruent to y x 2 2 and passes through (2, 2) and (5, 4) Determine its equation in vertex and standard form 15 The height of a ball thrown up in the air is given ash t t 49 294 12 Determine the maximum height reached by the ball and how long it took to get thereGraphing Parabolas Part 4 Graphing Recap Graphing by Completing the Square Intro Graphing by Completing the Square How Graphing by Completing the Square Freaky Things That Can Happen Making the Connection Between Graphing and Solving Coolmath privacy policy



From The Graph Of Y X 2 4 Draw The Graph Of Y 1 X 2 4



Unique Quadratic Equation In The Form Y Ax 2 Bx C
Consider the parabola y = x 2 Since all parabolas are similar, this simple case represents all others Construction and definitions The point E is an arbitrary point on the parabola The focus is F, the vertex is A (the origin), and the line FA is the axis of symmetry The line EC is parallel to the axis of symmetry and intersects the x axisWrite the new equation of the parabola y = = x?A parabola is symmetric about the vertex



Parabola Parent Function Mathbitsnotebook A1 Ccss Math




Consider A Parabola P That Is Congruent To Y X 2 Opens Upward And Has Vertex 0 0 Find The Brainly Com
The axis of symmetry of a parabola is a vertical line that divides the parabola into two congruent halves The axis of symmetry always passes through the vertex of the parabola The x coordinate of the vertex is the equation of the axis of symmetry of the parabola For a quadratic function in standard form, y = ax2 bx c , the axis ofIt is given that the vertex of parabola is at origin (0, 0) and it is symmetric about yaxis So, it's equation is x²= 4ay Or x² = –4ay Since the parabola passes




Plot A Graph For The Equation Y X 2 4x 1




2 Marks 4 If The Point 2 7 Is On The Parabola Y Chegg Com
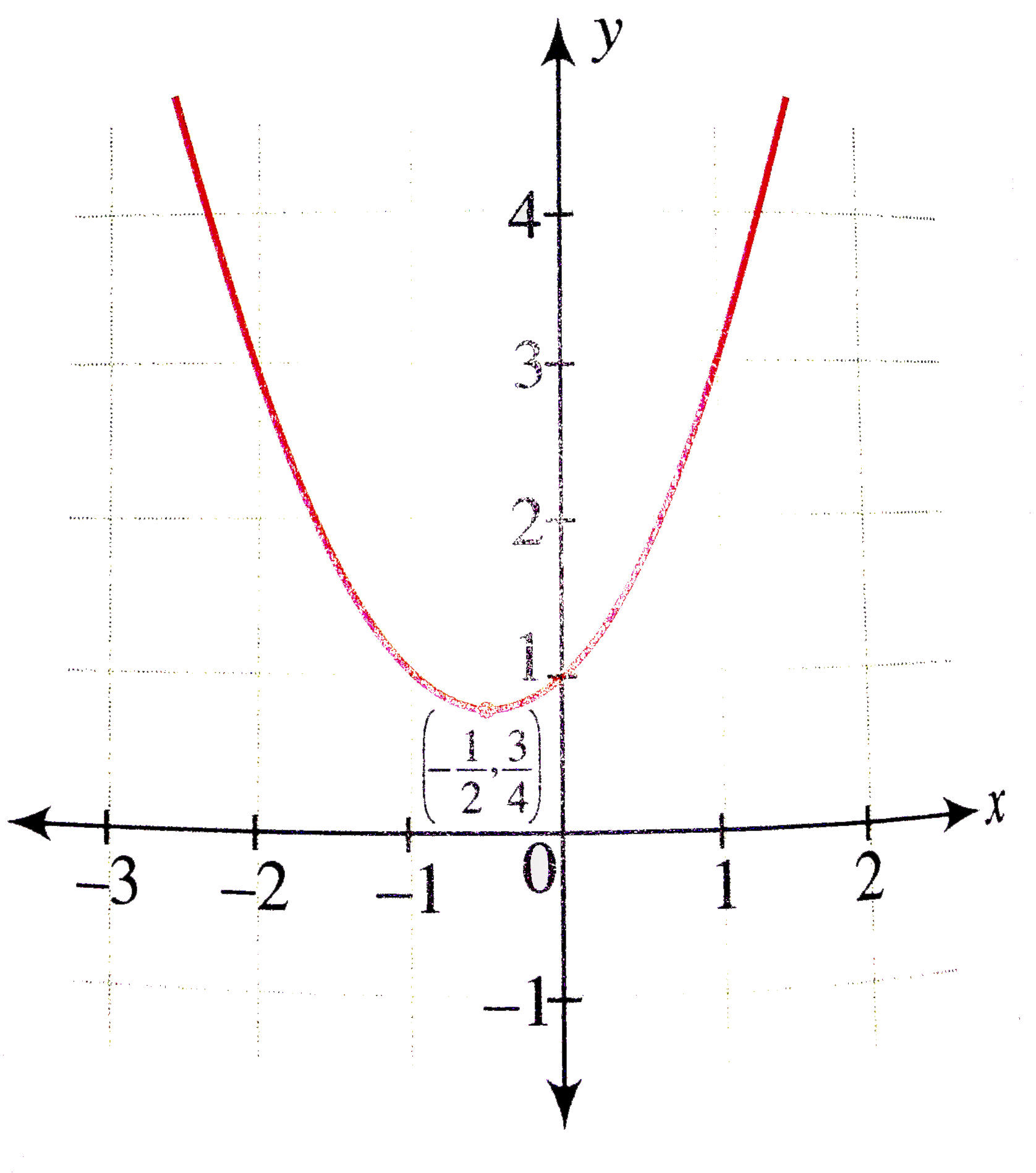



Draw The Graphs Of Following Quadratic Functions I Y X 2
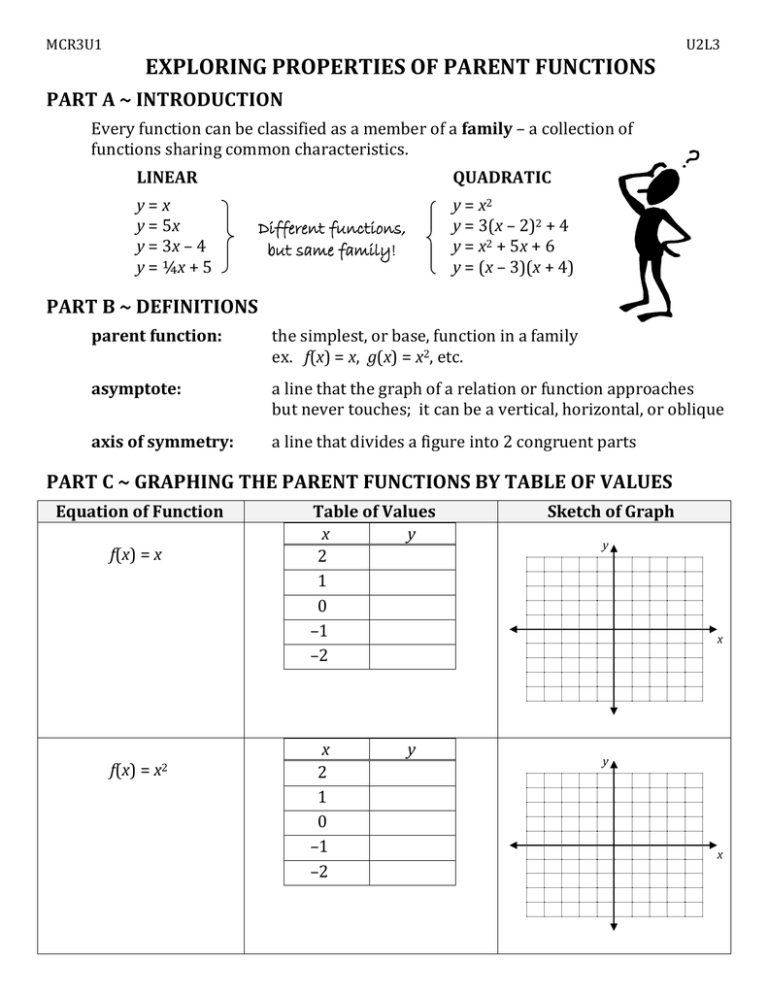



Exploring Properties Of Parent Functions Part A Introduction
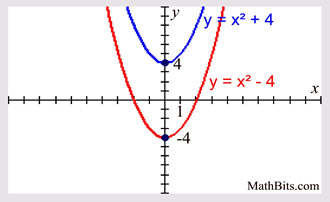



Parabola Parent Function Mathbitsnotebook A1 Ccss Math
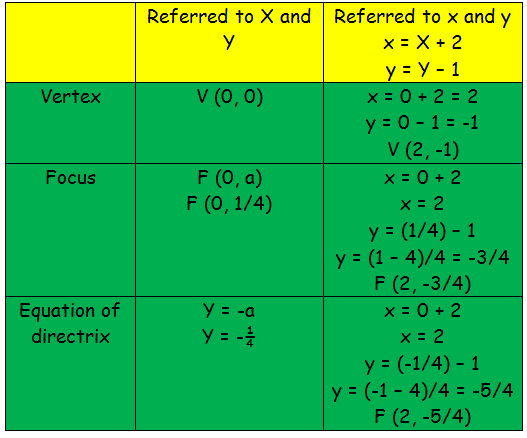



How To Find Focus Directrix And Vertex Of Parabola



Http Blessedmotherteresa Typepad Com Files Graphingquadratics Day3 Pdf



Math Spoken Here Classes Quadratic Equations 3



Consider A Parabola P That Is Congruent To Y X2 An Gauthmath
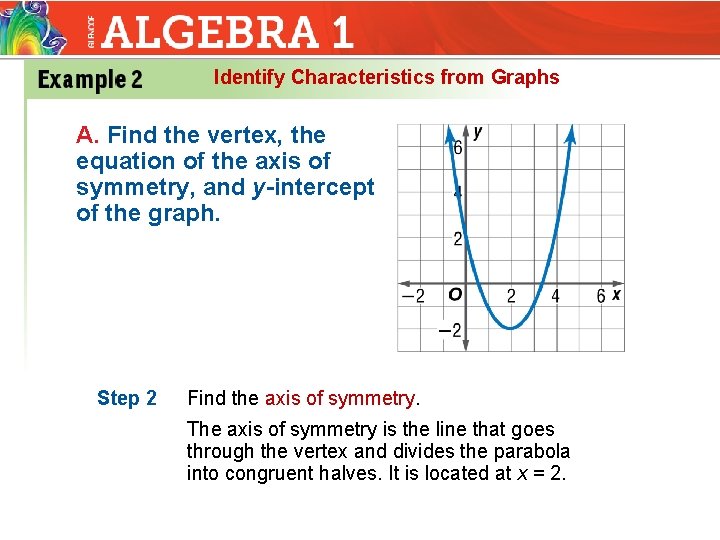



9 1 Identifying The Characteristics Of And Graphing



Http Mrhudson Pbworks Com W File Fetch Quadratic functions booklet Pdf




Resourceaholic Tricks And Tips 3 Quadratics



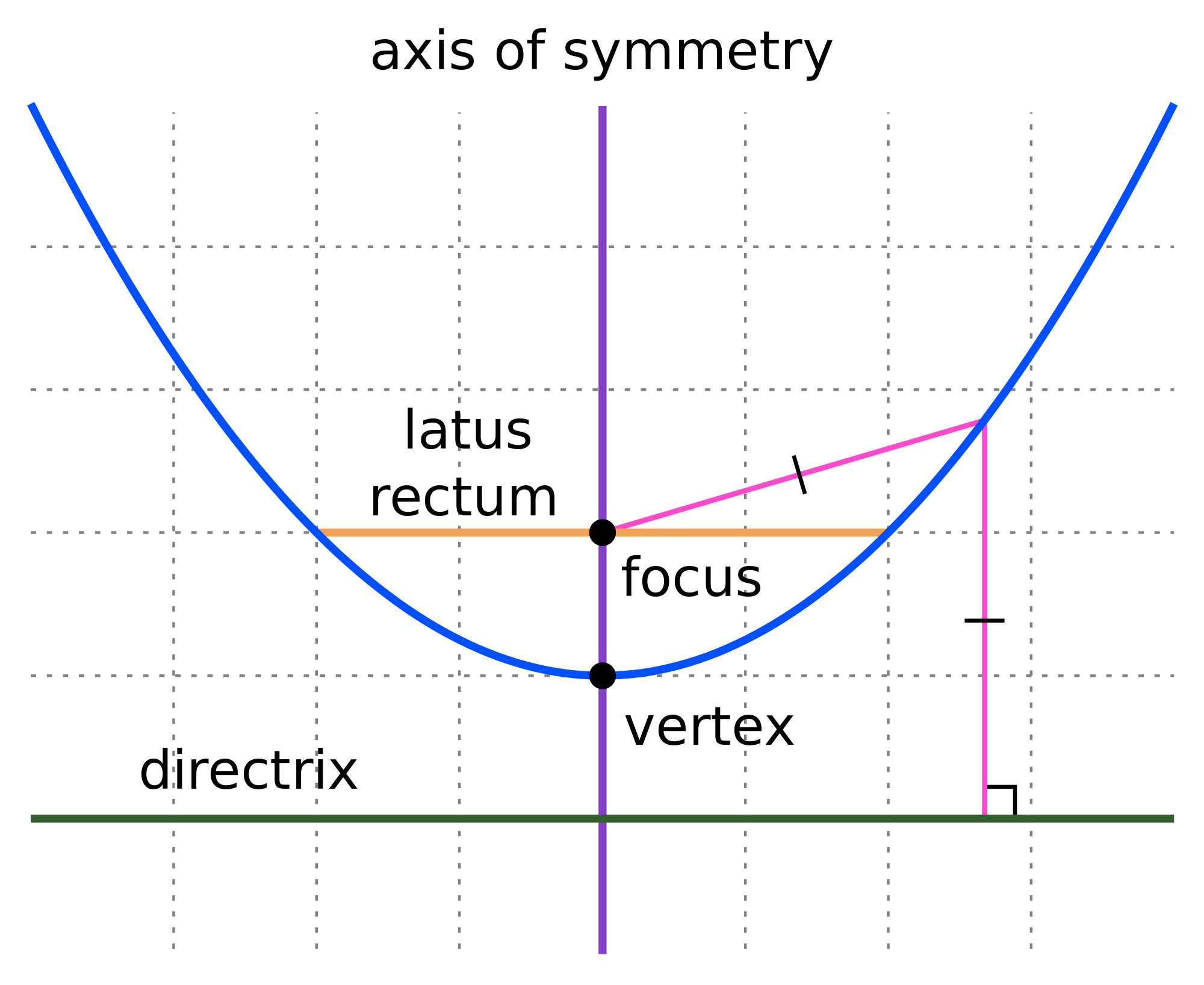
9 1 Identifying The Characteristics Of And Graphing



Parabola Wikipedia




Algebra Ii Module 1 Topic C Lesson 35 Student Version



Graphing Quadratic Functions




Quadratic Function




Consider A Parabola P That Is Congruent To Y X2 An Gauthmath




Lesson 4 2 Graphing Parabolas Using Transformations Ppt Download
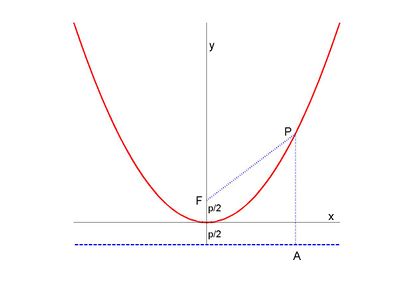



Parabola Knowino




Shifting Parabolas Video Khan Academy



Unique Quadratic Equation In The Form Y Ax 2 Bx C




Chap 7 The Parabola Pdf Quadratic Equation Geometry



L2d2ii Html




Solved Hand 9 Write The Equation For Each Parabola With Chegg Com




Graphing Quadratic Functions Lesson Article Khan Academy
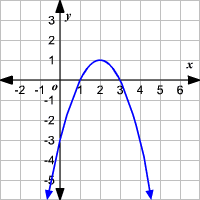



Axis Of Symmetry Of A Parabola




Chapter 4 Quadratics 4 3 Using Technology To Investigate Transformations Ppt Download
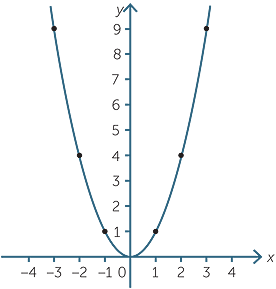



Quadratic Function




Attributes Of Quadratic Flashcards Quizlet




Parabola
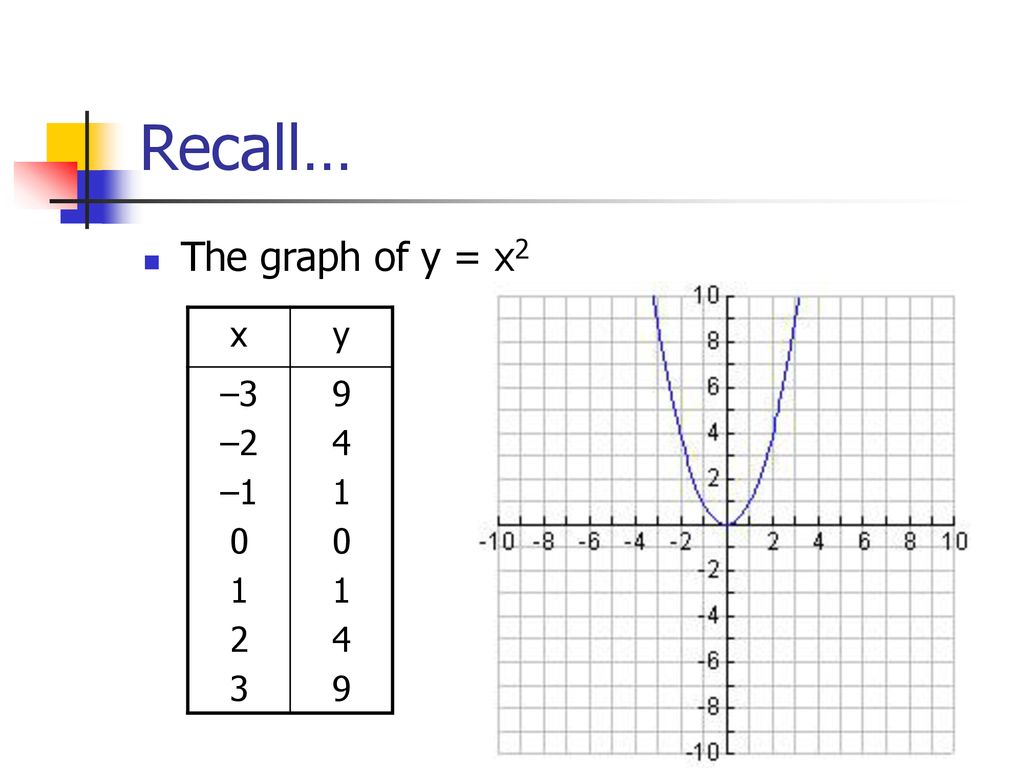



Lesson 4 2 Graphing Parabolas Using Transformations Ppt Download




Quadratic Functions Academic Support Center
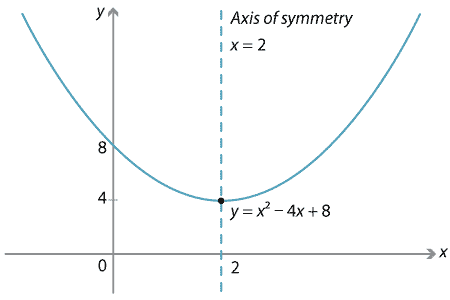



Content Transformations Of The Parabola
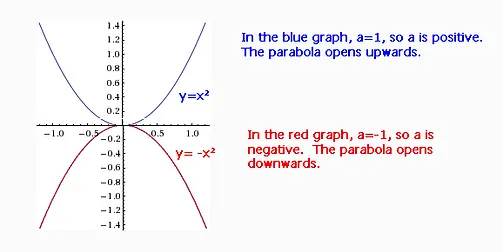



Vertex Form Chapter 4 Quad Relationships
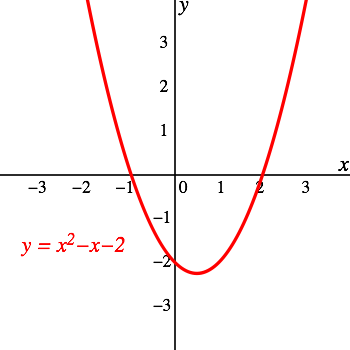



Graphs Of Quadratic Functions Boundless Algebra
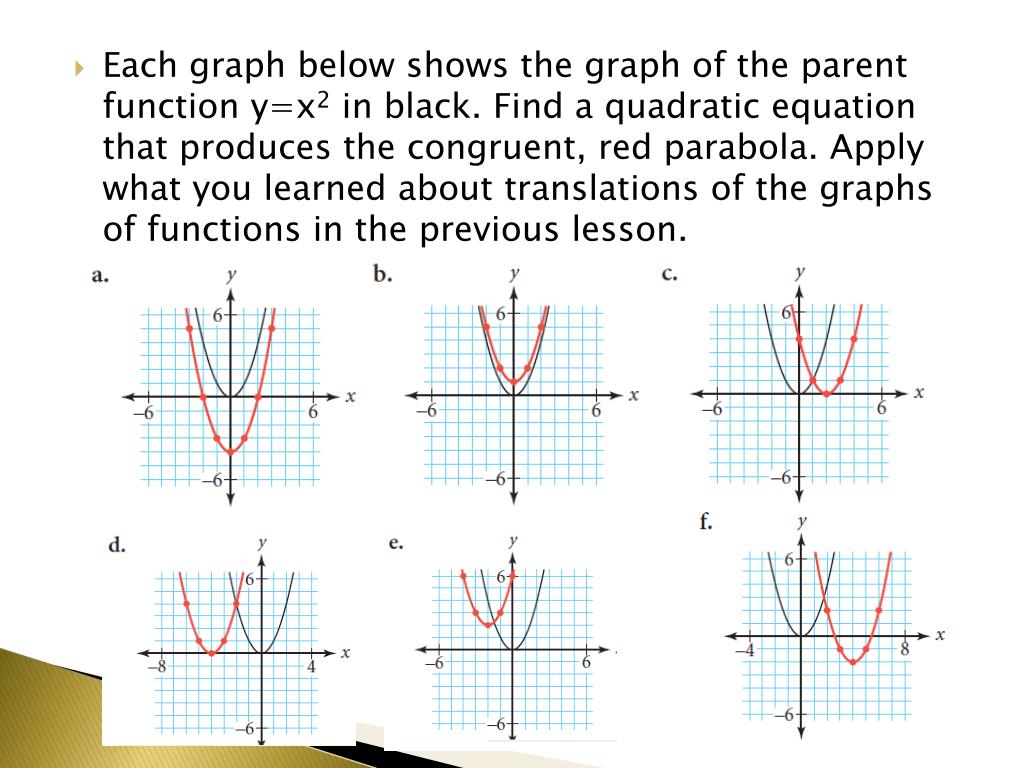



Ppt Translating And The Quadratic Family Powerpoint Presentation Free Download Id



What Is The Equation Of The New Parabola Created By Shifting Y X2 Three Units In The Positive Y Axis Direction Quora



The Parabola



2



1
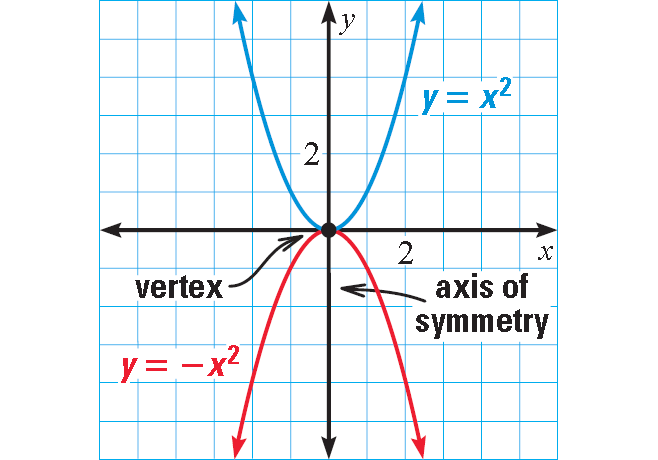



Graphing Quadratic Functions Parabola




Parabola Wikipedia



Solution Can You Help Me With This Problem A Parabola Is Congruent To Y X 2 And Has X Intercepts 1 And 5 Determine The Coordinates Of The Vertex




1 Point 17 Which Equation Describes A Parabola That Chegg Com
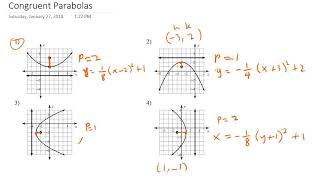



Congruent Parabolas Youtube



Www Engageny Org File Download Algebra Ii M1 Topic C Lesson 34 Teacher Pdf Token D04trqow




Chapter 4 Quadratics 4 3 Using Technology To Investigate Transformations Ppt Download




Resourceaholic Tricks And Tips 3 Quadratics
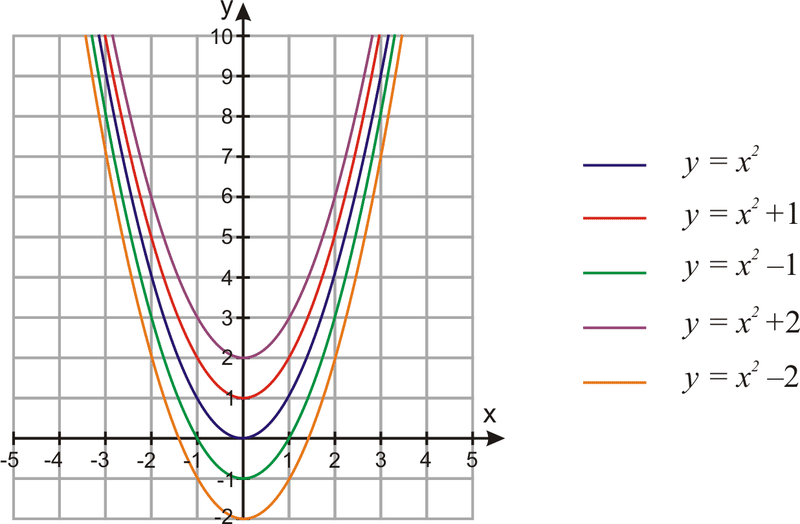



Vertical Shifts Of Quadratic Functions Ck 12 Foundation



Graphing Quadratic Functions



1




How To Find The Vertex Of A Quadratic Equation 10 Steps




Answered The Focus Of A Parabola Is 3 5 And Bartleby
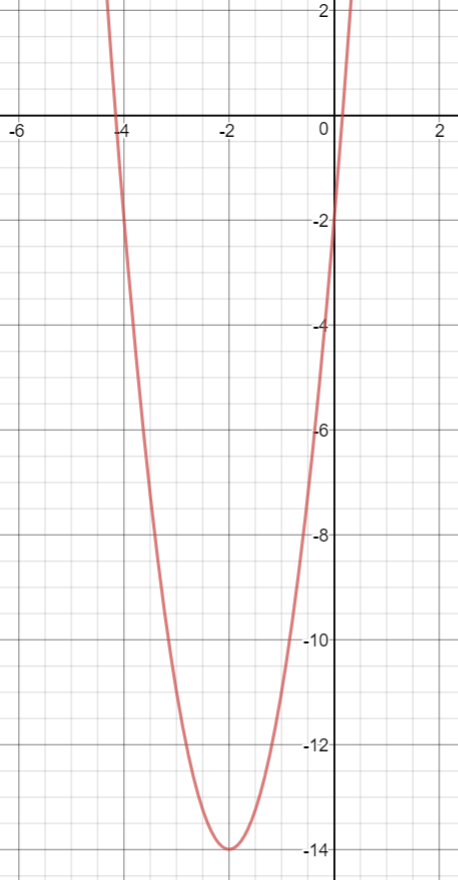



What Is The Axis Of Symmetry And Vertex For The Graph Y 3x 2 12x 2 Socratic
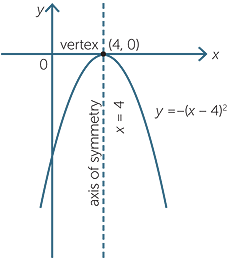



Quadratic Function
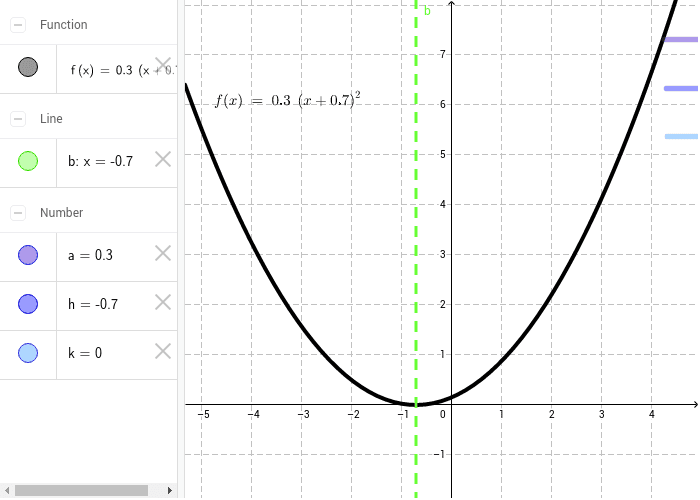



Transformations To The Graph Of Y X 2 Geogebra




Parabola Wikipedia
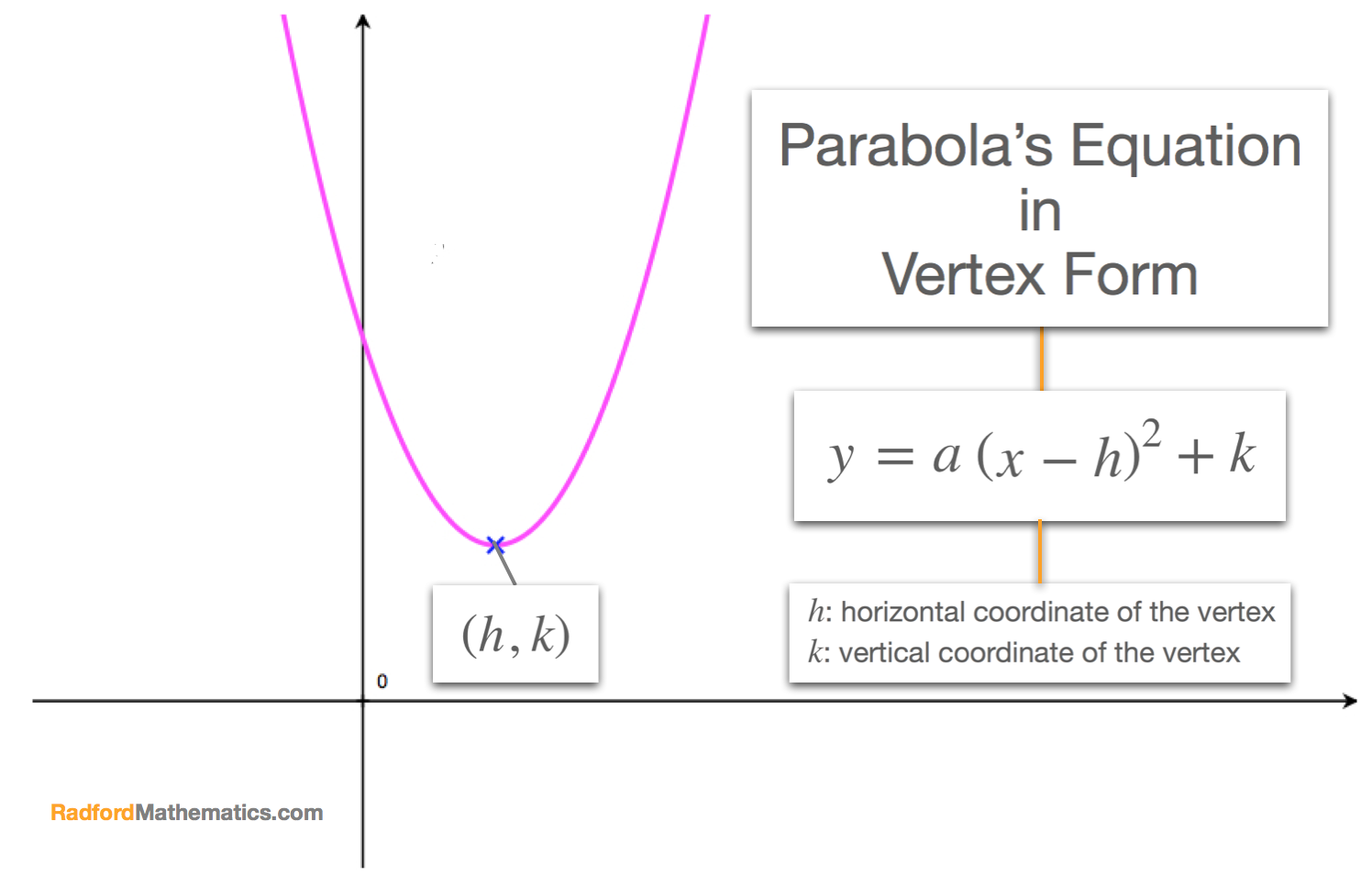



Vertex Form How To Find The Equation Of A Parabola
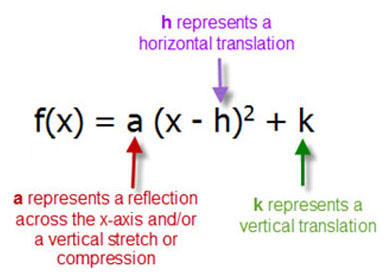



Untitled Document
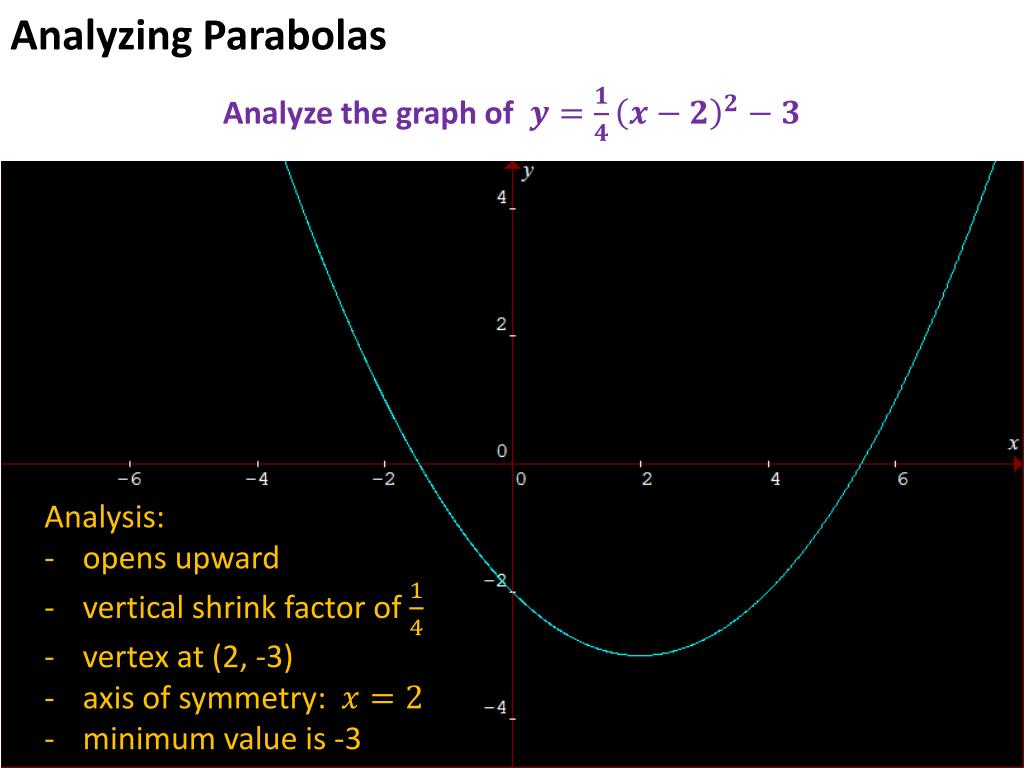



Ppt Analyzing Parabolas Powerpoint Presentation Free Download Id
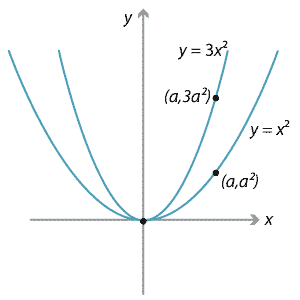



Content Transformations Of The Parabola
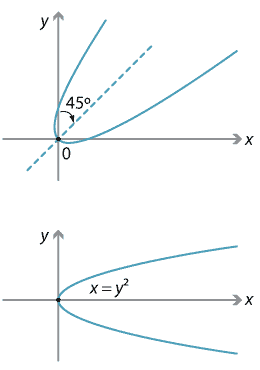



Content Transformations Of The Parabola




Quadratic Functions Academic Support Center




Graphing Quadratic Functions Lesson Article Khan Academy




Solved 1 4 Write The Equation For Each Parabola With The Chegg Com



Graphing Quadratic Functions



What Is The Maximum Vertical Distance Between The Line Math Y X 2 Math And The Parabola Math Y X 2 Math For Math 1 Le X Le 2 Math Quora
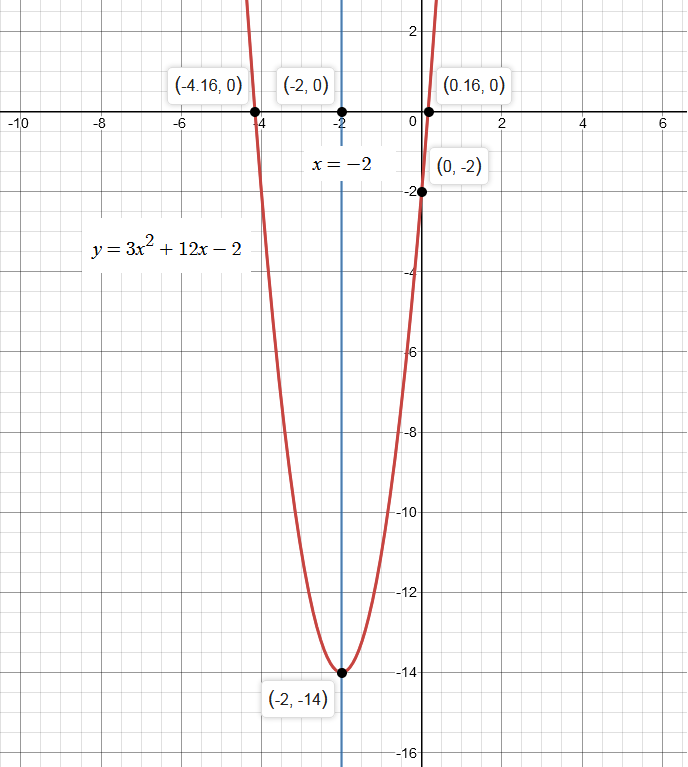



What Is The Axis Of Symmetry And Vertex For The Graph Y 3x 2 12x 2 Socratic




How To Find The Vertex Of A Quadratic Equation 10 Steps



Math Spoken Here Classes Quadratic Equations 3
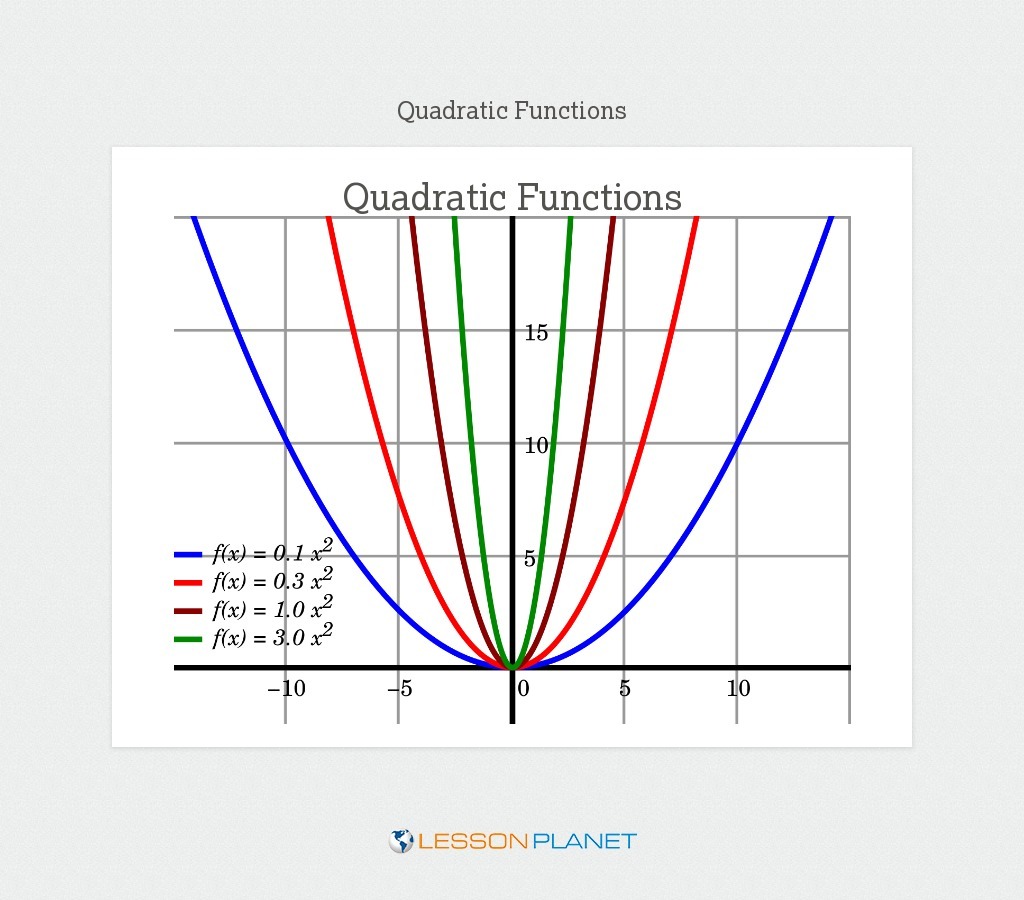



Parabola Lesson Plans Worksheets Lesson Planet
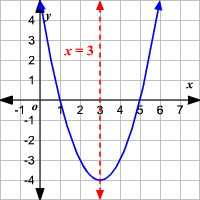



Axis Of Symmetry Of A Parabola




How To Find The Vertex Of A Quadratic Equation 10 Steps




Axis Of Symmetry Of A Parabola



What Transformations Are Needed To Transform The Graph Of The Parabola Y X 2 Into The Graph Of The Parabola Y X 2 4x 6 Quora



コメント
コメントを投稿